广州华商学院人工智能学院教师马雪婕于2024年12月27日在知名学术期刊《AIMS Mathematics》发表了题为 “A hybrid approach to conjugate gradient algorithms for nonlinear systems of equations with applications in signal restoration” 的研究论文。该期刊在数学领域具有重要影响力,该期刊属于SCIE检索期刊,是JCR Q1分区,中科院三区。

在诸多实际应用场景,如神经网络优化、图像分割、信号处理、矩阵方程求解及化学平衡分析等领域,带凸约束的非线性方程组都占据着关键地位。传统求解此类方程组的数值迭代方法主要分为依赖雅可比矩阵及其近似的方法和不依赖该矩阵的方法。前者虽在适当初始点下局部收敛迅速,但存在计算和存储雅可比矩阵的难题;后者虽结构简单、无需矩阵存储且适合大规模问题求解,但也面临着如收敛速度慢、性能不稳定等挑战。
马雪婕的研究针对这些问题提出了一种新颖的混合PRP - HS - LS 型共轭梯度算法(MPHL)。该算法具有多方面优势:
共轭参数构建:巧妙运用混合技术构造共轭参数,融合了PRP、HS 和 LS 共轭梯度方法的优点,有效提升了算法性能与稳定性,使其能更好地适应不同类型的非线性方程组求解需求。

图1. 共轭参数构建
搜索方向优势:基于所构建的共轭参数设计的搜索方向,无需线搜索机制即可满足充分下降和信赖域性质。这一特性不仅简化了算法流程,还减少了计算量,在大规模问题求解中优势尤为突出。

图2. 搜索方向设计
全局收敛突破:在一般假设条件下,成功证明了算法的全局收敛性,且突破了传统方法中对Lipschitz 连续性条件的依赖。这使得该算法能够应用于更广泛的问题类型,极大地拓展了其应用范围。

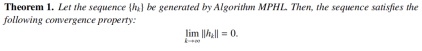
图3. 收敛性分析
实验验证有效:通过大量数值实验,在约束非线性方程组和稀疏信号恢复问题上对算法进行了全面测试。实验结果表明,MPHL算法在求解大规模约束非线性方程组和处理稀疏信号恢复问题时表现卓越。与现有算法相比,在多个测试案例中,MPHL 算法在CPU时间、函数评估次数和迭代次数等性能指标上均具有明显优势,展现出更高的效率和有效性。
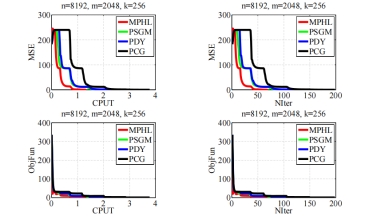
图4.四种算法在信号尺寸(n, m, k)=(8192,2048,256)时的比较结果
本论文是马雪婕在相关研究领域的重要成果,为非线性方程组求解及信号恢复研究提供了新的思路与方法,有望推动相关领域的进一步发展,并在实际工程应用中发挥重要作用。其研究得到了广西自然科学基金(项目编号:2024GXNSFAA010478)和广州华商学院导师项目(项目编号:2024HSDS15)的大力支持。
来源:人工智能学院